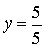Equações de primeiro grau
(com uma variável)
Introdução
Equação é toda sentença matemática aberta que exprime uma relação de igualdade. A palavra equação tem o prefixo equa, que em latim quer dizer "igual". Exemplos:
2x + 8 = 0
5x - 4 = 6x + 8
3a - b - c = 0
Não são equações:
4 + 8 = 7 + 5 (Não é uma sentença aberta)
x - 5 < 3 (Não é igualdade)
![]() (não é sentença aberta, nem igualdade)
(não é sentença aberta, nem igualdade)
A equação geral do primeiro grau:
ax+b = 0
onde a e b são números conhecidos e a diferente de 0, se resolve de maneira simples: subtraindo b dos dois lados, obtemos:
ax = -b
dividindo agora por a (dos dois lados), temos:
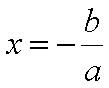
Considera a equação 2x - 8 = 3x -10
A letra é a incógnita da equação. A palavra incógnita significa " desconhecida".
Na equação acima a incógnita é x; tudo que antecede o sinal da igualdade denomina-se 1º membro, e o que sucede, 2º membro.
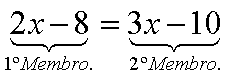
Qualquer parcela, do 1º ou do 2º membro, é um termo da equação.
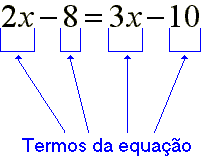
| Equação do 1º grau na incógnita x é toda equação que pode ser escrita na forma ax=b, sendo a e b números racionais, com a diferente de zero. |
Conjunto Verdade e Conjunto Universo de uma Equação
Considere o conjunto A = {0, 1, 2, 3, 4, 5} e a equação x + 2 = 5.
Observe que o número 3 do conjunto A é denominado conjunto universo da equação e o conjunto {3} é o conjunto verdade dessa mesma equação.
Observe este outro exemplo:
-
Determine os números inteiros que satisfazem a equação x² = 25
O conjunto dos números inteiro é o conjunto universo da equação.
Os números -5 e 5, que satisfazem a equação, formam o conjunto verdade, podendo ser indicado por: V = {-5, 5}.
Daí concluímos que:
| Conjunto Universo é o conjunto de todos os valores que variável pode assumir. Indica-se por U. |
| Conjunto verdade é o conjunto dos valores de U, que tornam verdadeira a equação . Indica-se por V. |
Observações:
- O conjunto verdade é subconjunto do conjunto universo.
![]()
- Não sendo citado o conjunto universo, devemos considerar como conjunto universo o conjunto dos números racionais.
![]()
O conjunto verdade é também conhecido por conjunto solução e pode ser indicado por S.
Raízes de uma equação
Os elementos do conjunto verdade de uma equação são chamados raízes da equação.
Para verificar se um número é raiz de uma equação, devemos obedecer à seguinte seqüência:
-
Substituir a incógnita por esse número.
-
Determinar o valor de cada membro da equação.
-
Verificar a igualdade, sendo uma sentença verdadeira, o número considerado é raiz da equação.
Exemplos:
Verifique quais dos elementos do conjunto universo são raízes das equações abaixo, determinando em cada caso o conjunto verdade.
-
Resolva a equação x - 2 = 0, sendo U = {0, 1, 2, 3}.
Para x = 0 na equação x - 2 = 0 temos: 0 - 2 = 0 => -2 = 0. (F)
Para x = 1 na equação x - 2 = 0 temos: 1 - 2 = 0 => -1 = 0. (F)
Para x = 2 na equação x - 2 = 0 temos: 2 - 2 = 0 => 0 = 0. (V)
Para x = 3 na equação x - 2 = 0 temos: 3 - 2 = 0 => 1 = 0. (F)
Verificamos que 2 é raiz da equação x - 2 = 0, logo V = {2}.
-
Resolva a equação 2x - 5 = 1, sendo U = {-1, 0, 1, 2}.
Para x = -1 na equação 2x - 5 = 1 temos: 2 . (-1) - 5 = 1 => -7 = 1. (F)
Para x = 0 na equação 2x - 5 = 1 temos: 2 . 0 - 5 = 1 => -5 = 1. (F)
Para x = 1 na equação 2x - 5 = 1 temos: 2 . 1 - 5 = 1 => -3 = 1. (F)
Para x = 2 na equação 2x - 5 = 1 temos: 2 . 2 - 5 = 1 => -1 = 1. (F)
A equação 2x - 5 = 1 não possui raiz em U, logo V = Ø.
Resolução de uma equação
Resolver uma equação consiste em realizar uma espécie de operações de operações que nos conduzem a equações equivalentes cada vez mais simples e que nos permitem, finalmente, determinar os elementos do conjunto verdade ou as raízes da equação. Resumindo:
|
Resolver uma equação significa determinar o seu conjunto verdade, dentro do conjunto universo considerado. |
Na resolução de uma equação do 1º grau com uma incógnita, devemos aplicar os princípios de equivalência das igualdades (aditivo e multiplicativo). Exemplos:
-
Sendo
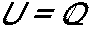 , resolva a equação
, resolva a equação 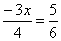 .
.
MMC (4, 6) = 12
![]()
-9x = 10 => Multiplicador por (-1)
9x = -10
![]()
Como ![]() , então
, então ![]() .
.
-
Sendo
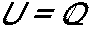 , resolva a equação 2 . (x - 2) - 3 . (1 - x) = 2 . (x - 4).
, resolva a equação 2 . (x - 2) - 3 . (1 - x) = 2 . (x - 4).
Iniciamos aplicando a propriedade distributiva da multiplicação:
2x - 4 - 3 + 3x = 2x - 8
2x + 3x -2x = - 8 + 4 + 3
3x = -1
![]()
Como 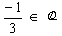 , então
, então 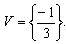
Equações impossíveis e identidades
-
Sendo
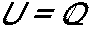 , considere a seguinte equação: 2 . (6x - 4) = 3 . (4x - 1).
, considere a seguinte equação: 2 . (6x - 4) = 3 . (4x - 1).
Observe, agora, a sua resolução:
2 . 6x - 2 . 4 = 3 . 4x - 3 . 1
12x - 8 = 12x - 3
12x - 12x = - 3 + 8
0 . x = 5
Como nenhum número multiplicado por zero é igual a 5, dizemos que a equação é impossível e, portanto, não tem solução. Logo, V = Ø.
Assim, uma equação do tipo ax + b = 0 é impossível quando ![]() e
e ![]()
-
Sendo
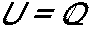 , considere a seguinte equação: 10 - 3x - 8 = 2 - 3x.
, considere a seguinte equação: 10 - 3x - 8 = 2 - 3x.
Observe a sua resolução:
-3x + 3x = 2 - 10 + 8
0 . x = 0
Como todo número multiplicado por zero é igual a zero, dizemos que a equação possui infinitas soluções. Equações desse tipo, em que qualquer valor atribuído à variável torna a equação verdadeira, são denominadas identidades.
Equações de 1º grau (com duas variáveis)
Pares ordenados
Muitas vezes, para localizar um ponto num plano, utilizamos dois números racionais, numa certa ordem.
Denominamos esses números de par ordenado. Exemplos:
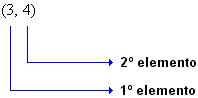
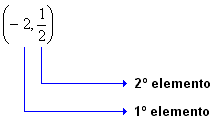
Assim:
|
Indicamos por (x, y) o par ordenado formado pelos elementos x e y, onde x é o 1º elemento e y é o 2º elemento. |
-
Observações
-
De um modo geral, sendo x e y dois números racionais quaisquer, temos:
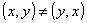 . Exemplos
. Exemplos
![]()
2. Dois pares ordenados (x, y) e (r, s) são iguais somente se x = r e y = s.
Representação gráfica de um Par Ordenado
Podemos representar um par ordenado através de um ponto em um plano.
Esse ponto é chamado de imagem do par ordenado.
Coordenadas Cartesianas
Os números do par ordenados são chamados coordenadas cartesianas. Exemplos:
A (3, 5) ==> 3 e 5 são as coordenadas do ponto A.
Denominamos de abscissa o 1º número do par ordenado, e ordenada, o 2º número desse par. Assim:

Plano Cartesiano
|
Representamos um par ordenado em um plano cartesiano. Esse plano é formado por duas retas, x e y, perpendiculares entre si. A reta horizontal é o eixo das abscissas (eixo x). A reta vertical é o eixo das ordenadas (eixo y). O ponto comum dessas duas retas é denominado origem, que corresponde ao par ordenado (0, 0). |
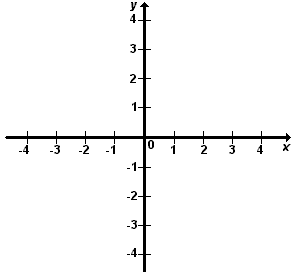 |
Localização de um Ponto
Para localizar um ponto num plano cartesiano, utilizamos a seqüência prática:
-
O 1º número do par ordenado deve ser localizado no eixo das abscissas.
-
O 2º número do par ordenado deve ser localizado no eixo das ordenadas.
-
No encontro das perpendiculares aos eixos x e y, por esses pontos, determinamos o ponto procurado. Exemplo:
-
Localize o ponto (4, 3).
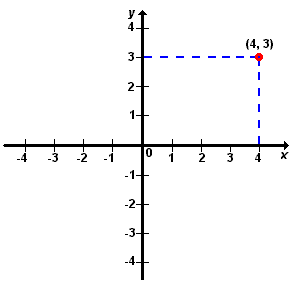
Produto Cartesiano
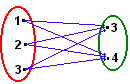
| Sejam os conjuntos A = {1, 2, 3} e B = {3, 4}.
Com auxílio do diagrama de flechas ao lado formaremos o conjunto de todos os pares ordenados em que o 1º elemento pertença ao conjunto A e o 2º pertença ao conjunto B. |
|
Assim , obtemos o conjunto: {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
Esse conjunto é denominado produto cartesiano de A por B, e é indicado por:
![]()
Logo:
Dados dois conjuntos A e B, não-vazios, denominamos produtos cartesiano A x B o conjunto de todos os pares ordenados (x, y) onde ![]()
![]()
Equações de primeiro grau
(com duas variáveis)
Considere a equação: 2x - 6 = 5 - 3y
Trata-se de uma equação com duas variáveis, x e y, pode ser transformada numa equação equivalente mais simples. Assim:
2x + 3y = 5 + 6
2x + 3y = 11 ==> Equação do 1º grau na forma ax + by = c .
| Denominando equação de 1º grau com duas variáveis, x e y, a toda equação que pode ser reproduzida à forma ax + by = c, sendo a e b números diferentes de zero, simultaneamente. |
Na equação ax + by = c, denominamos:
| x + y - variáveis ou incógnita
a - coeficiente de x |
b - coeficiente de y
c - termo independente |
Exemplos:
| x + y = 30
2x + 3y = 15 x - 4y = 10 |
-3x - 7y = -48
2x- 3y = 0 x - y = 8 |
Solução de uma equação de 1º grau com duas variáveis
Quais o valores de x e y que tornam a sentença x - 2y = 4 verdadeira?
Observe os pares abaixo:
x = 6, y = 1
|
x - 2y = 4 6 - 2 . 1 = 4 6 - 2 = 4 4 = 4 (V) |
x = 8, y = 2
|
x - 2y = 4 8 - 2 . 2 = 4 8 - 4 = 4 4 = 4 (V) |
x = -2, y = -3
|
x - 2y = 4 -2 - 2 . (-3) = 4 -2 + 6 = 4 4 = 4 (V) |
Verificamos que todos esses pares são soluções da equação x - 2y = 4.
Assim, os pares (6, 1); (8, 2); (-2, -3) são algumas das soluções dessa equação.
Uma equações do 1º grau com duas variáveis tem infinitas soluções - infinitos (x, y) - , sendo, portanto, seu conjunto universo  .
.
Podemos determinar essas soluções, atribuindo-se valores quaisquer para uma das variáveis, calculando a seguir o valor da outra. Exemplo:
-
Determine uma solução para a equação 3x - y = 8.
Atribuímos para o x o valor 1, e calculamos o valor de y. Assim:
|
3 . (1) - y = 8 3 - y = 8 -y = 5 ==> Multiplicamos por -1 y = -5 |
O par (1, -5) é uma das soluções dessa equação.
V = {(1, -5)}
Resumindo:
Um par ordenado (r, s) é solução de uma equação ax + by = c (a e b não-nulos simultaneamente), se para x = r e y = s a sentença é verdadeira.
Gráfico de uma equação de 1º grau com duas variáveis
Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções.
Cada uma dessas soluções pode ser representada por um par ordenado (x, y).
Dispondo de dois pares ordenados de um equação, podemos representá-los graficamente num plano cartesiano, determinando, através da reta que os une, o conjunto das solução dessa equação. Exemplo:
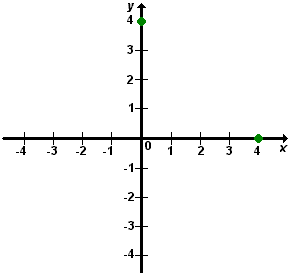
- Construir um gráfico da equação x + y = 4.
Inicialmente, escolhemos dois pares ordenados que solucionam essa equação.
1º par: A (4, 0)
2º par: B (0, 4)
A seguir, representamos esses pontos num plano cartesiano.
|
|
Finalmente, unimos os pontos A e B, determinando a reta r, que contém todos os pontos soluções da equação.
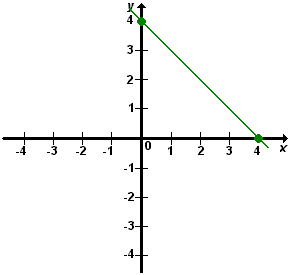 |
A reta r é chamada reta suporte do gráfico da equação.
Sistemas de Equações
Considere o seguinte problema:
Pipoca, em sua última partida, acertou x arremessos de 2 pontos e y arremessos de 3 pontos. Ele acertou 25 arremessos e marcou 55 pontos. Quantos arremessos de 3 pontos ele acertou?
Podemos traduzir essa situação através de duas equações, a saber:
x + y = 25 (total de arremessos certo)
2x + 3y = 55 (total de pontos obtidos)
Essas equações contém um sistema de equações.
Costuma-se indicar o sistema usando chave.
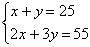
O par ordenado (20, 5), que torna ambas as sentenças verdadeiras, é chamado solução do sistema. Um sistema de duas equações com duas variáveis possui uma única solução.
Resolução de Sistemas
A resolução de um sistema de duas equações com duas variáveis consiste em determinar um par ordenado que torne verdadeiras, ao mesmo tempo, essas equações.
Estudaremos a seguir alguns métodos:
Método de substituição
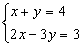
Solução
-
determinamos o valor de x na 1ª equação.
x = 4 - y
- Substituímos esse valor na 2ª equação.
2 . (4 - y) -3y = 3
- Resolvemos a equação formada.
|
8 - 2y -3y = 3 8 - 2y -3y = 3 -5y = -5 => Multiplicamos por -1 5y = 5 y = 1 |
- Substituímos o valor encontrado de y, em qualquer das equações, determinando x.
|
x + 1 = 4 x = 4 - 1 x = 3 |
- A solução do sistema é o par ordenado (3, 1).
V = {(3, 1)}
Método da adição
Sendo U =  , observe a solução de cada um dos sistemas a seguir, pelo método da adição.
, observe a solução de cada um dos sistemas a seguir, pelo método da adição.
Resolva o sistema abaixo:
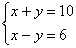
Solução
-
Adicionamos membros a membros as equações:
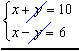
2x = 16
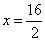
x = 8
-
Substituímos o valor encontrado de x, em qualquer das equações, determinado y:
8 + y = 10
y = 10 - 8
y = 2
A solução do sistema é o par ordenado (8, 2)
V = {(8, 2)}
Gráfico de uma equação de 1º grau com duas variáveis
Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções.
Cada uma dessas soluções pode ser representada por um par ordenado (x, y).
Dispondo de dois pares ordenados de um equação, podemos representá-los graficamente num plano cartesiano, determinando, através da reta que os une, o conjunto das solução dessa equação. Exemplo:
- Construir um gráfico da equação x + y = 4.
Inicialmente, escolhemos dois pares ordenados que solucionam essa equação.
1º par: A (4, 0)
2º par: B (0, 4)
A seguir, representamos esses pontos num plano cartesiano.
|
|
Finalmente, unimos os pontos A e B, determinando a reta r, que contém todos os pontos soluções da equação.
 |
A reta r é chamada reta suporte do gráfico da equação.
Sistemas de Equações
Considere o seguinte problema:
Pipoca, em sua última partida, acertou x arremessos de 2 pontos e y arremessos de 3 pontos. Ele acertou 25 arremessos e marcou 55 pontos. Quantos arremessos de 3 pontos ele acertou?
Podemos traduzir essa situação através de duas equações, a saber:
x + y = 25 (total de arremessos certo)
2x + 3y = 55 (total de pontos obtidos)
Essas equações contém um sistema de equações.
Costuma-se indicar o sistema usando chave.
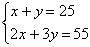
O par ordenado (20, 5), que torna ambas as sentenças verdadeiras, é chamado solução do sistema. Um sistema de duas equações com duas variáveis possui uma única solução.
Resolução de Sistemas
A resolução de um sistema de duas equações com duas variáveis consiste em determinar um par ordenado que torne verdadeiras, ao mesmo tempo, essas equações.
Estudaremos a seguir alguns métodos:
Método de substituição
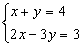
Solução
-
determinamos o valor de x na 1ª equação.
x = 4 - y
- Substituímos esse valor na 2ª equação.
2 . (4 - y) -3y = 3
- Resolvemos a equação formada.
|
8 - 2y -3y = 3 8 - 2y -3y = 3 -5y = -5 => Multiplicamos por -1 5y = 5 y = 1 |
- Substituímos o valor encontrado de y, em qualquer das equações, determinando x.
|
x + 1 = 4 x = 4 - 1 x = 3 |
- A solução do sistema é o par ordenado (3, 1).
V = {(3, 1)}
Método da adição
Sendo U =  , observe a solução de cada um dos sistemas a seguir, pelo método da adição.
, observe a solução de cada um dos sistemas a seguir, pelo método da adição.
Resolva o sistema abaixo:
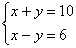
Solução
-
Adicionamos membros a membros as equações:
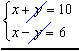
2x = 16
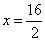
x = 8
-
Substituímos o valor encontrado de x, em qualquer das equações, determinado y:
8 + y = 10
y = 10 - 8
y = 2
A solução do sistema é o par ordenado (8, 2)
V = {(8, 2)}
Inequações de primeiro grau
Introdução
|
Denominamos inequação toda sentença matemática aberta por uma desigualdade. |
As inequações do 1º grau com uma variável podem ser escritas numa das seguintes formas:
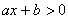 ,
, 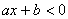 ,
, 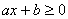 ,
, 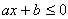 , como a e b reais
, como a e b reais 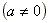 . Exemplos:
. Exemplos:
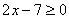 |
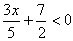 |
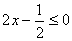 |
Representação gráfica de uma inequação do 1º grau com duas variáveis
Método prático
-
Substituímos a desigualdade por uma igualdade.
-
Traçamos a reta no plano cartesiano.
-
Escolhemos um ponto auxiliar, de preferência o ponto (0, 0) e verificamos se o mesmo satisfaz ou não a desigualdade inicial.
Em caso positivo, a solução da inequação corresponde ao semiplano ao qual pertence o ponto auxiliar.
Em caso negativo, a solução da inequação corresponde ao semiplano oposto aquele ao qual pertence o ponto auxiliar. Exemplos:
-
Representamos graficamente a inequação
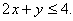
|
Tabela
|
 |
Substituindo o ponto auxiliar (0, 0) na inequação 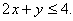
Verificamos:
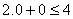
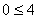 (Afirmativa positiva, o ponto auxiliar satisfaz a inequação)
(Afirmativa positiva, o ponto auxiliar satisfaz a inequação)
A solução da inequação corresponde ao semiplano ao qual pertence o ponto auxiliar (0, 0).
Inequações de primeiro grau
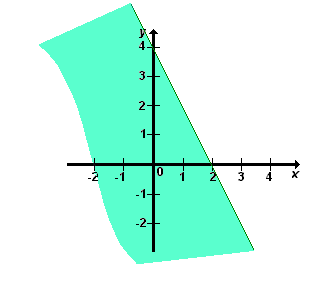
Resolução Gráfica de um Sistema de Inequações do 1º grau
Para resolver um sistema de inequações do 1º grau graficamente, devemos:
-
traçar num mesmo plano o gráfico de cada inequação;
-
determinar a região correspondente à intersecção dos dois semiplanos. Exemplos:
-
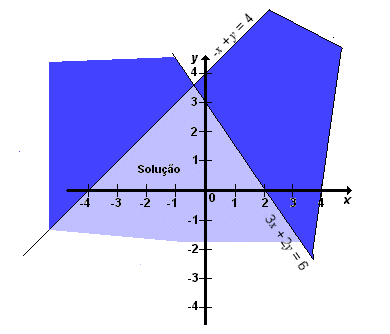
Dê a resolução gráfica do sistema:
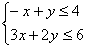
Solução
Traçando as retas -x + y = 4 e 3x + 2y = 6.
|
Tabela
Tabela
|
Gráfico
|