O Cálculo Diferencial e Integral, também chamado de cálculo infinitesimal, ou simplesmente Cálculo, é um ramo importante da matemática, desenvolvido a partir da Álgebra e da Geometria, que se dedica ao estudo de taxas de variação de grandezas (como a inclinação de uma reta) e a acumulação de quantidades (como a área debaixo de uma curva ou o volume de um sólido). Onde há movimento ou crescimento e onde forças variáveis agem produzindo aceleração, o cálculo é a matemática a ser empregada.
O cálculo foi criado como uma ferramenta auxiliar em várias áreas das ciências exatas. Desenvolvido por Isaac Newton (1643-1727) e Gottfried Wilhelm Leibniz (1646-1716), em trabalhos independentes. O Cálculo auxilia em vários conceitos e definições na matemática, química, física clássica, física moderna e economia. O estudante de cálculo deve ter um conhecimento em certas áreas da matemática, como funções, geometria e trigonometria, pois são a base do cálculo. O cálculo tem inicialmente três "operações-base", ou seja, possui áreas iniciais como o cálculo de limites, o cálculo de derivadas de funções e a integral de diferenciais.
A integral indefinida também pode ser chamada de antiderivada, uma vez que é um processo que inverte a derivada de funções. Já a integral definida, inicialmente definida como Soma de Riemann, estabelece limites de integração, ou seja, é um processo estabelecido entre dois intervalos bem definidos, daí o nome integral definida.
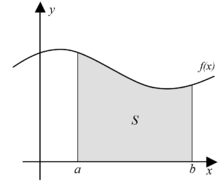
O cálculo permite calcular a área da região assinalada.
Com o advento do "Teorema Fundamental do Cálculo" estabeleceu-se uma conexão entre os dois ramos do cálculo: o Cálculo Diferencial e o Cálculo Integral. O cálculo diferencial surgiu do problema da tangente, enquanto o cálculo integral surgiu de um problema aparentemente não relacionado, o problema da área. O professor de Isaac Newton em Cambridge, Isaac Barrow, descobriu que esses dois problemas estão de fato estritamente relacionados, ao perceber que a derivação e a integração são processos inversos. Foram Leibniz e Newton que exploraram essa relação e a utilizaram para transformar o cálculo em um método matemático sistemático. Particularmente ambos viram que o Teorema Fundamental os capacitou a calcular áreas e integrais muito mais facilmente, sem que fosse necessário calculá-las como limites de soma (método descrito pelo matemático Riemann, pupilo de Gauss).
A história do cálculo encaixa-se em vários períodos distintos, de forma notável nas eras antiga, medieval e moderna.
História
Na Antiguidade, foram introduzidas algumas ideias do cálculo integral, embora não tenha havido um desenvolvimento dessas ideias de forma rigorosa e sistemática. A função básica do cálculo integral, calcular volumes e áreas, pode ser remontada ao Papiro Egípcio de Moscou (1850 A.C.), no qual um egípcio trabalhou o volume de um frustum piramidal. Eudoxo de Cnido, ou Eudoxus, (408-355 a.C.) usou o método da exaustão para calcular áreas e volumes. Arquimedes (287-212 a.C.) levou essa ideia além, inventando a heurística, que se aproxima do cálculo integral. O método da exaustão foi redescoberto na China por Liu Hui no século III, que o usou para encontrar a área do círculo. O método também foi usado por Zu Chongzhi século V, para achar o volume de uma esfera.
Na Idade Média, o matemático indiano Aryabhata usou a noção infinitesimal em 499 d.C. expressando-a em um problema de astronomia na forma de uma equação diferencial básica. Essa equação levou Bhāskara II no século XII a desenvolver uma derivada prematura representando uma mudança infinitesimal, e ele desenvolveu também o que seria uma forma primitiva do "Teorema de Rolle". No século XII, o matemático persa Sharaf al-Din al-Tusi descobriu a derivada de polinômios cúbicos, um resultado importante no cálculo diferencial. No século XIV, Madhava de Sangamagrama, juntamente com outros matemáticos-astrônomos da Escola Kerala de Astronomia e Matemática, descreveu casos especiais da Série de Taylor, que no texto são tratadas como Yuktibhasa.
Na Idade Moderna, descobertas independentes no cálculo foram feitas no início do século XVII no Japão por matemáticos como Seki Kowa, que expandiu o método de exaustão. Na Europa, a segunda metade do século XVII foi uma época de grandes inovações. O Cálculo abriu novas oportunidades na física-matemática de resolver problemas muito antigos que até então não haviam sido solucionados. Muitos matemáticos contribuíram para essas descobertas, notavelmente John Wallis e Isaac Barrow. James Gregory proveu um caso especial do segundo teorema fundamental do cálculo em 1668. Coube a Gottfried Wilhelm Leibniz e a Isaac Newton recolher essas ideias e juntá-las em um corpo teórico que viria a constituir o cálculo. A ambos é atribuída a simultânea e independente invenção do cálculo. Leibnitz foi originalmente acusado de plagiar os trabalhos não publicados de Isaac Newton; hoje, porém, é considerado o inventor do cálculo, juntamente com Newton. Historicamente Newton foi o primeiro a aplicar o cálculo à física ao passo que Leibniz desenvolveu a notação utilizada até os dias de hoje, a notação de Leibniz. O argumento histórico para conferir aos dois a invenção do cálculo é que ambos chegaram de maneiras distintas ao teorema fundamental do cálculo.

De acordo com Gauss, Arquimedes, o maior matemático da antiguidade, já apresentava ideias relacionadas ao Cálculo dois séculos antes de Cristo.

Sir Isaac Newton aplicou o cálculo às suas leis do movimento e a outros conceitos matemáticos-físicos.
Quando Newton e Leibniz publicaram seus resultados, houve uma grande controvérsia de qual matemático (e portanto que país: Inglaterra ou Alemanha) merecia o crédito. Newton derivou seus resultados primeiro, mas Leibniz publicou primeiro. Newton argumentou que Leibniz roubou ideias de seus escritos não publicados, que Newton à época compartilhara com alguns poucos membros da Sociedade Real. Esta controvérsia dividiu os matemáticos ingleses dos matemáticos alemães por muitos anos. Um exame cuidadoso dos escritos de Leibniz e Newton mostra que ambos chegaram a seus resultados independentemente, com Leibniz iniciando com integração e Newton com diferenciação. Nos dias de hoje tem-se que Newton e Leibniz descobriram o cálculo independentemente. Leibniz, porém, foi quem deu o nome cálculo à nova disciplina, Newton a chamara de "A ciência dos fluxos". Desde o tempo de Leibniz e Newton, muitos matemáticos contribuíram para o contínuo desenvolvimento do cálculo.

Gottfried Wilhelm Leibniz: o inventor do cálculo, juntamente com Newton
Na Idade Contemporânea, já no século XIX, o cálculo foi abordado de uma forma muito mais rigorosa. Foi também durante este período que ideias do cálculo foram generalizadas ao espaço euclidiano e ao plano complexo. Lebesgue mais tarde generalizou a noção de integral. Sobressaíram matemáticos como Cauchy, Riemann, Weierstrass e Maria Gaetana Agnesi. Esta foi autora da primeira obra a unir as ideias de Isaac Newton e Gottfried Wilhelm Leibniz; escreveu também um dos primeiros livros sobre cálculo diferencial e integral 1 . É dela também a autoria da chamada "curva de Agnesi".

Maria Gaetana Agnesi
Princípios
Limites e Infinitesimais
O cálculo é comumente utilizado pela manipulação de quantidades muito pequenas. Historicamente, o primeiro método de utilizá-lo era pelas infinitesimais. Estes objetos podem ser tratados como números que são, de alguma forma, "infinitamente pequenos". Na linha numérica, isso seria locais onde não é zero, mas possui "zero" de distância de zero. Nenhum número diferente de zero é um infinitesimal, porque sua distância de zero é positiva. Qualquer múltiplo de um infinitesimal continua sendo um infinitesimal. Em outras palavras, infinitesimais não satisfazem a propriedade Archimediana. Deste ponto de vista, o cálculo é uma coleção de técnicas para manipular infinitesimais. Tal pensamento foi ignorado no século XIX porque era muito difícil ter a noção precisa de uma infinitesimal. Entretanto, o conceito foi reutilizado no século XX com a introdução da análise não padronizada, a qual propiciou fundamentos sólidos para a manipulação de infinitesimais
No século XIX, as infinitesimais foram substituídas pelos limites. Limites descrevem o valor de uma função em um certo ponto em termos dos valores de pontos próximos. Eles capturam o comportamento numérico em baixa escala, como nas infinitesimais, mas utilizando números ordinários. Deste ponto de vista, calculo é uma coleção de técnicas para a manipulação de certos limites. As infinitesimais foram substituídas por números muito pequenos, e o comportamento infinitamente pequeno da função é encontrado pelo limite de números cada vez menores. Limites são fáceis de serem colocados em fundações rigorosas e, por esse motivo, são a abordagem padrão para o cálculo.
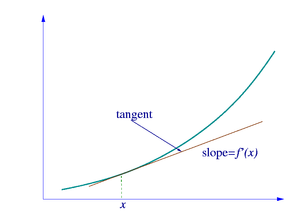
O cálculo diferencial é o estudo da definição, propriedade e aplicações da derivada ou deslocamento de um gráfico. O processo de encontrar a derivada é chamado "diferenciação". Em linguagem técnica, a derivada é um operador linear, o qual forma uma nova função a partir da função original, em que cada ponto da nova função é o deslocamento da função original. O conceito de derivada é fundamentalmente mais avançado do que os conceitos encontrados em álgebra. Nessa matéria, os estudantes aprendem sobre funções em que o número de entrada gera um número de saída. Por exemplo, se no dobro da função é inserido 3, então a saída é 6, enquanto se a função é quadrática, e é inserido 3, então a saída é 9. Mas na derivada, a entrada é uma função e a saída é outra função. Por exemplo, se na derivada é colocada uma função quadrada, então a saída é o dobro de uma função, porque o dobro da função fornece o deslocamento da função quadrática em qualquer ponto dado da função. Para entender a derivada, os estudantes precisam aprender a notação matemática. Na notação matemática, um símbolo comum para a derivada da função é um sinal de apóstrofo chamado "linha". Então a derivada de f é f ' (f linha). Isso em notação matemática seria escrito assim:

Se a função de entrada é o tempo, então a derivada dessa função é a taxa em que a função é alterada.
Se a função é linear, ou seja, o gráfico da função é uma linha reta, então a função pode ser escrita como y = m x + b, onde:
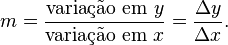
Isto da o valor exato para a variação da linha reta. Se a função não é uma linha reta, então a variação em y é dividida pela variação em x, e nós precisamos do cálculo para encontrar o valor exato em cada ponto da função. (Note que y e f(x) são duas notações diferentes para a mesma coisa: a saída da função). Uma linha entre dois pontos em uma curva é chamado de reta secante. A variação da reta secante pode ser expressada como:

onde as coordenadas do primeiro ponto é (x, f(x)) e h é a distância horizontal entre os dois pontos.
Para determinar o deslocamento da curva, nós usamos os limites:
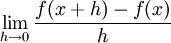
Em um caso particular, nós encontramos o deslocamento da função quadrática no ponto em que a entrada é 3 e a saída é 9 (Ex.:  então
então  ).
).

O deslocamento da função quadrática no ponto (3, 9) é 6, isto é, ele cresce seis vezes mais rápido em y do que em x e está indo para a direita.
Integrais
O Cálculo Integral é o estudo das definições, propriedades, e aplicações de dois conceitos relacionados, as integrais indefinidas e as integrais definidas. O processo de encontrar o valor de uma integral é chamado integração. Em linguagem técnica, o calculo integral estuda dois operadores lineares relacionados.
A integral indefinida é a antiderivada, o processo inverso da derivada. F é uma integral indefinida de f quando f é uma derivada de F. (O uso de letras maiúsculas e minúsculas para uma função e sua integral indefinida é comum em cálculo.)
A integral definida insere uma função e extrai um número, o qual fornece a área entre o gráfico da função e o eixo do x. A definição técnica da integral definida é o limite da soma das áreas dos retângulos, chamada Soma de Riemann.
Um exemplo motivacional é a distância (D) viajada em um determinado tempo (t).
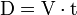
Se a velocidade (V) é constante, somente multiplicação é necessária, mas se a velocidade varia, então precisamos de um método mais poderoso para encontrar a distância. Um método é a aproximação da distância viajada pela divisão do tempo em muito mais intervalos de tempo, e então multiplicando o tempo em cada intervalo por uma das velocidades naquele intervalo, e então fazer uma Soma de Riemann das distâncias aproximadas viajadas em cada intervalo. A ideia básica é que se somente um pequeno tempo passar, então a velocidade vai permanecer praticamente a mesma. Entretanto, uma Soma de Riemann somente da uma aproximação da distância viajada. Nós precisamos pegar o limite de todas as Somas de Riemann para encontrar a distância viajada exata.
Se f(x) no diagrama da esquerda representa a velocidade variando de acordo com o tempo, a distância viajada entre os tempos representados por a e b é a área da região escura s.
Para aproximar a área, um método intuitivo seria dividir em distâncias entre a e b em um número de segmentos iguais, a distância de cada segmento representado pelo símbolo ?x. Para cada segmento menor, nós podemos escolher um valor da função f(x). Chame o valor h. Então a área do retângulo com a base ?x e altura h dá a distância (tempo ?x multiplicado pela velocidade h) viajado naquele segmento. Associado com cada segmento é o valor médio da função sobre ela,f(x)=h. A soma de todos os retângulos dados é uma aproximação da área entre o eixo e a curva, o qual é uma aproximação da distância total viajada. Um valor menor para ?x nos dará mais retângulos e, na maioria dos casos uma melhor aproximação, mas para uma resposta exata nós precisamos fazer o limite em ?x tender a zero.
O símbolo da integração é  um S alongado (que significa "soma"). A integral definida é escrita da forma:
um S alongado (que significa "soma"). A integral definida é escrita da forma:
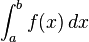
e lida como "a integral de a até b de f-de-x em relação a x."
A integral indefinida, ou antiderivada, é escrita da forma:
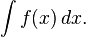
Desde que a derivada da função y = x² + C é y ' = 2x (onde C é qualquer constante), então:

Conceitos básicos
Função, domínio e imagem
Seja um conjunto de pontos A, cujos membros são os números em  então tomamos
então tomamos  e denominamo-la variável independente, visto que, arbitrariamente, lhe podemos atribuir qualquer valor em
e denominamo-la variável independente, visto que, arbitrariamente, lhe podemos atribuir qualquer valor em  e portanto dizemos que:
e portanto dizemos que:
A é o domínio da variável  2
2
Da mesma forma, admitamos um conjunto de pontos B, cujos membros são números que são obtidos única e exclusivamente por um conjunto de regras matemáticas  , quando números arbitrários em A lhe são transferidos; visto que há um único valor assumido para cada valor arbitrário transferido a
, quando números arbitrários em A lhe são transferidos; visto que há um único valor assumido para cada valor arbitrário transferido a  , dizemos que:
, dizemos que:
B é função de A.
Sendo B obtido através das regras de 
A é domínio da função 
Da mesma forma, como B é restrito aos valores definidos por A e às regras definidas por 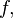 os seus elementos espelham estas condições, portanto, podemos dizer que:
os seus elementos espelham estas condições, portanto, podemos dizer que:
B é imagem da função 
Extensões de domínios
Observemos a expressão:  Note que assim que atribuirmos valores a
Note que assim que atribuirmos valores a  a mesma assumirá valores inválidos, valores de raízes quadradas de números negativos, para sanar este problema, poderemos atribuir uma faixa de valores válidos para o domínio de
a mesma assumirá valores inválidos, valores de raízes quadradas de números negativos, para sanar este problema, poderemos atribuir uma faixa de valores válidos para o domínio de  então teremos:
então teremos:

Assim, teremos um domínio restrito a valores iguais ou menores que 12, portanto, incluindo-o, este extremo ao qual pertence o valor 12 chamamos de extremo fechado.
Temos uma situação semelhante, porém com uma sutil diferença, quando temos que fazer:  neste caso, temos que restringir o valor 0 e todos os números abaixo dele, desta forma:
neste caso, temos que restringir o valor 0 e todos os números abaixo dele, desta forma:

Poderemos atribuir apenas valores maiores que 0, uma vez que este valor não pertence ao conjunto de números que podem ser atribuídos à variável, chamamos este de extremo aberto.
Notações
O conjunto de números B  dos quais
dos quais  dependem do conjunto A
dependem do conjunto A  de onde temos
de onde temos  estabelecemos o par de números
estabelecemos o par de números  ou simplesmente:
ou simplesmente:

Este é chamado de par ordenado.
Sendo também  a representação dos valores de
a representação dos valores de  então podemos dizer que:
então podemos dizer que:

Sendo  o valor de
o valor de  quando definido pelas operações em
quando definido pelas operações em 
Faixas de valores que delimitam os domínios podem ser representados com desigualdades, como nos exemplos abaixo:

Porém, os extremos podem ser colocados em um par entre delimitadores de forma que, para os extremos fechados usamos os delimitadores [ ou ], para os extremos abertos usamos ( ou ), habilitando-nos a identificar os extremos mais claramente, desta forma podemos identificar os domínios do exemplo acima desta forma:

Também é comum usar colchetes invertidos para extremos abertos:
![]-2, 4[; [-12, 8[](https://upload.wikimedia.org/math/5/6/3/5630442908bb4e177e4b54c00fb9ce51.png)
Operações com funções
Consideremos duas funções f e g; admitindo que as duas são, intuitivamente, expressões que se traduzem em valores, podemos dizer que:



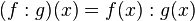
Sendo D(f) o domínio da função f e D(g) o domínio da função g, o domínio da função resultante das operações acima é sempre:

Teorema Fundamental do Cálculo
O teorema fundamental do cálculo afirma que a diferenciação e a integração são operações inversas. Mais precisamente, o teorema conecta os valores de antiderivadas ao valor de integrais definidas. Por ser usualmente mais fácil computar uma antiderivada do que aplicar a definição de uma integral definida, o teorema fundamental do cálculo provê uma forma prática de computar integrais definidas. Pode também ser interpretado como uma afirmação precisa do fato que a diferenciação é o inverso da integração.
É afirmado pelo teorema fundamental do cálculo que: Se uma função f é contínua no intervalo [a, b] e se F é uma função cuja derivada é f no intervalo (a, b), então
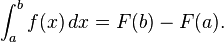
Além disso, para cada x no intervalo (a, b) temos que
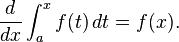
E, seu Corolário pode ser transcrito da seguinte forma:
Considere f uma função contínua de valores reais definida em um intervalo fechado [a, b]. Se F é uma função tal que  para todo x em [a, b]
para todo x em [a, b]
então

e

Essa descoberta, realizada por Newton e Leibniz, que se basearam nos resultados de um trabalho anterior de Isaac Barrow, exerceu um papel chave na massiva proliferação de resultados analíticos que se seguiram após seus trabalhos ficarem conhecidos. O Teorema fundamental do cálculo provê um método algébrico de computar muitas integrais definidas sem executar processos limite—simplesmente por encontrar fórmula para antiderivadas.
Aplicações
O cálculo é usado em todos os ramos das ciências físicas, na ciência da computação, estatística, engenharia, economia, medicina e em outras áreas sempre que um problema possa ser modelado matematicamente e uma solução ótima é desejada. A Física faz uso intensivo do cálculo. Todos os conceitos na mecânica clássica são interrelacionados pelo cálculo. A massa de um objeto de densidade conhecida, o momento de inércia dos objetos, assim como a energia total de um objeto dentro de um sistema fechado podem ser encontrados usando o cálculo. Nos sub-campos da eletricidade e magnetismo, o cálculo pode ser usado para encontrar o fluxo total de campos eletromagnéticos. Um exemplo mais histórico do uso do cálculo na física é a segunda lei de Newton que usa a expressão "taxa de variação" que se refere à derivada: A taxa de variação do momento de um corpo é igual à força resultante que age sobre o corpo e na mesma direção. Até a expressão comum da segunda lei de Newton como Força = Massa × Aceleração envolve o cálculo diferencial porque a aceleração pode ser expressada como a derivada da velocidade. A teoria do eletromagnetismo de Maxwell e a teoria da relatividade geral de Einstein também são expressas na linguagem do cálculo diferencial. A química também usa o cálculo para determinar as variações na velocidade das reações e no decaimento radioativo. O cálculo pode ser usado em conjunto com outras disciplinas matemáticas. Por exemplo, ele pode ser usado com a álgebra linear para encontrar a reta que melhor representa um conjunto de pontos em um domínio. Na esfera da medicina, o cálculo pode ser usado para encontrar o ângulo ótimo na ramificação dos vasos sanguíneos para maximizar a circulação, e até mesmo determinar o tamanho máximo de moléculas que são capazes de atravessar a membrana plasmática em uma determinada situação, normal ou induzida, em células. Na geometria analítica, o estudo dos gráficos de funções, o cálculo é usado para encontrar pontos máximos e mínimos, a inclinação, concavidade e pontos de inflexão. Na economia o cálculo permite a determinação do lucro máximo fornecendo uma fórmula para calcular facilmente tanto o custo marginal quanto a renda marginal. O cálculo pode ser usado para encontrar soluções aproximadas de equações, em métodos como o método de Newton, iteração de ponto fixo e aproximação linear. Por exemplo, naves espaciais usam uma variação do método de Euler para aproximar trajetórias curvas em ambientes de queda livre.
Cálculo diferencial e integral 4.1
Introdução
O conceito de limite e continuidade é um conceito importante na definição de derivada e integral. Neste capítulo trabalhamos com limite, continuidade, derivada e integral utilizando os comando do Mathematica. Abordamos também a derivada de ordem superior, derivada parcial, derivada das funções implícitas e integração múltipla.
4.2 Conceito de limite
Iniciamos este capítulo com o cálculo de limites. O comando utilizado em Mathematica para este cálculo é "Limit[expressão,x->x0]". Também utilizamos a opção "Direction", o que permite o cálculo de limites laterais, isto é, à direita e à esquerda. Veja os exemplos a seguir:
Exemplo 4.1 Calcular os seguinte limites:
a) ![]() , onde
, onde ![]() ;
;
b) ![]() ;
;
c) ![]() , onde f(x) é dada como em a).
, onde f(x) é dada como em a).
Resolução Utilizamos o comando "Limit" para resolver estes exemplos:
a) In[ ]:= f[x_]:=(- 5+3 x+4 x^2)/(10- 5 x+8 x^2)
Limit[f[x],x->5] Out[ ]=![]()
b) In[ ]:= Limit[(1+x)^(1/x),x->0]
Out[ ]= E
c) In[ ]:= Limit[f[x],x->Infinity]
Out[ ]= ![]()
Assim, concluímos que

 =
=  ;
; = e;
= e;
 =
= .
.
A seguir apresentamos exemplos de cálculo de limites à direita e à esquerda.
Assim, concluímos que

 =
=  ;
; = e;
= e;
 =
= .
.
A seguir apresentamos exemplos de cálculo de limites à direita e à esquerda.
Exemplo 4.2
Calcular os seguintes limites à direita e à esquerda:
a)  ;
;
b) ![]() .
.
Faça a visualização gráfica de cada uma destas funções.
Resolução
Para calcular os limites direcionados utilizamos a opção "Direction" juntamente com o comando "Limit":
a) In[ ]:= f[x_]:=(4- x^2)/(2- x)
In[ ]:= Limit[f[x],x->2,Direction-> -1]
Out[ ]= 4
In[ ]:= Limit[f[x],x->2,Direction->1]
Out[ ]= 4
Assim, concluímos que
 ;
;
isto é,
 .
.
Veja a seguir, o gráfico da função dada:
In[ ]:= Plot[(4- x^2)/(2- x),{x,0,3}]

Out[ ]= -Graphics-
b) In[ ]:= Limit[1/x,x->0,Direction-> -1]
Out[ ]= Infinity
In[ ]:= Limit[1/x,x->0,Direction-> 1]
Out[ ]= -Infinity
Assim, concluímos que
 e
e 
isto é,
não existe.
A visualização gráfica desta função é obtida usando o comando "Plot".
In[ ]:= Plot[1/x,{x,- 1,1}]

Out[ ]= -Graphics-
Observamos no gráfico acima que o limite da função no ponto x = 0 não existe.
O exemplo a seguir nos leva a definir o conceito de derivada utilizando o aspecto de limite.
Exemplo 4.3
Calcular ![]() , onde
, onde
a) f1(x) = 4x3 ![]() 2x2 - x
2x2 - x ![]() 3;
3;
b) f2(x) = ![]() .
.
Resolução
Utilizamos os seguintes comandos para calcular os limites desejados:
a) In[ ]:= Clear[f1]
f1[x_]:=4 x^3+2 x^2- x+3
In[ ]:= k1=Simplify[(f1[x+h]- f1[x])/h]
Out[ ]= -1+2 h + 4 h2 + 4 x + 12 h x + 12 x2
In[ ]:= Limit[k1,h->0]
Out[ ]= -1 + 4 x + 12 x2
b) In[ ]:= Clear[f2]
f2[x_]:=(x^2+1)/x
In[ ]:= k2=Simplify[(f2[x+h]-f2[x])/h]
Out[ ]= ![]()
![]()
In[ ]:= Limit[k2,h->0]
Out[ ]= ![]()
Assim, concluímos que
 ;
;
 .
.
O exemplo acima nos leva a definir o conceito de derivada de uma função, o que veremos na próxima seção.
Seja uma função diferenciável f(x), isto é, que tem derivada, definida por
![]()
O Mathematica poderá computar sua derivada de pelo menos duas formas, desde que a função f(x) tenha sido definida de maneira adequada. Inicialmente calculamos a derivada usando a definição.
Seguem abaixo alguns comandos para se calcular derivadas:
- O comando "f�[x]" computa a derivada de f(x) em relação a x.
- O comando "D[f[x],x]" também computa a derivada de f(x) e relação a x.
- O comando "D[f[x],{x,n}]" computa a n-ésima derivada de f(x) em relação a x.
- O comando "D[expressão,variável]" computa a derivada da expressão em relação a variável.
Exemplo 4.4
Calcular a derivada da expressão 7x - 9x2 ![]() 8x3.
8x3.
Resolução
Para se calcular a derivada da expressão 7x - 9x2 + 8x3, podemos derivar diretamente ou podemos definir uma função f(x) = 7x - 9x2 + 8x3. Os comandos abaixo calculam a derivada da mesma função de três formas diferentes:
1a forma
In[ ]:= D[7 x- 9 x^2+8 x^3,x]
Out[ ]= 7 - 18 x + 24 x2
2a forma
In[ ]:= Clear[h]
h[x_]:=7 x- 9 x^2+8 x^3
In[ ]:= h'[x]
Out[ ]= 7 - 18 x + 24 x2
3a forma
In[ ]:= D[h[x],x]
Out[ ]= 7 - 18 x + 24 x2
Observe que tanto "h�[x]" quanto "D[h[x],x]" produziram o mesmo resultado.
Assim, concluímos que
- (7x - 9x2
 8x3)¢ = 7 - 18x
8x3)¢ = 7 - 18x  24x2.
24x2.
Exemplo 4.5
Calcular a derivada das seguintes funções
a) f(x) = x2 sen x;
b) f(x) = ln(3x4 ![]() 4);
4);
c) f(x) = (5x ![]() 3)(2x3 - 3x
3)(2x3 - 3x ![]() 4)2.
4)2.
Resolução
Resolvemos estes exemplos utilizando os comando "D" dado no exemplo acima.
a) In[ ]:= D[x^2 Sin[x],x]
Out[ ]= x2 Cos[x] + 2 x Sin[x]
b) In[ ]:= D[Log[3 x^4 + 4],x]
Out[ ]= ![]()
c) In[ ]:= D[(5 x+3)(2 x^3- 3 x+4),x]
Out[ ]= (3 + 5 x)(- 3 + 6 x2) + 5(4 - 3 x + 2 x3)
Assim, concluímos que
- (x2 sen x)¢ = x2 cos(x)
 2x sen(x);
2x sen(x); - (ln(3x4
 4))¢ =
4))¢ =  ;
; - ((5x
 3)(2x3 - 3x
3)(2x3 - 3x  4)2)¢ = (3
4)2)¢ = (3  5x)(- 3
5x)(- 3  6x2)
6x2)  5(4 - 3x
5(4 - 3x  2x3).
2x3).
Exemplo 4.6
Calcular f¢ (x), f¢ ¢ (x) e f¢ ¢ ¢ (x) para as seguintes funções:
a) f(x) = x4 - 3x3 ![]() 5x2
5x2 ![]() 3x
3x![]() 1;
1;
b) f(x) = ![]() .
.
Resolução
Utilizamos os seguintes comandos para resolver estes exemplos:
a) In[ ]:= Clear[f]
f[x_]:= x^4- 3 x^3+5 x^2+3 x+1
In[ ]:= D[f[x],x]
Out[ ]= 3 + 10 x - 9 x2 + 4 x3
In[ ]:= D[f[x],{x,2}]
Out[ ]= 10 - 18 x + 12 x2
In[ ]:= D[f[x],{x,3}]
Out[ ]= -18 + 24 x
Assim, concluímos que
- f¢ (x) = 3
 10x - 9x2
10x - 9x2  4x3;
4x3; - f¢ ¢ (x) = 10 - 18x
 12x2;
12x2; - f¢ ¢ ¢ (x) = - 18
 24x.
24x.
b) In[ ]:= Clear[f]
f[x_]:=(Sin[4 x])/x
In[ ]:= D[f[x],x]
Out[ ]= ![]()
In[ ]:= D[f[x],{x,2}]
Out[ ]= ![]()
In[ ]:= D[f[x],{x,3}]
Out[ ]= ![]()
Assim, concluímos que
- f¢ (x) =
 ;
; - f¢ ¢ (x) =
 ;
; - f¢ ¢ ¢ (x) =
 .
.
4.3.1 Derivadas da função implícita
Utilizando os comandos do Mathematica podemos calcular a derivada da função implícita f(x,y) = 0. Os principais comandos são os seguintes:
- O comando "Dt[equação,x]" computa a diferencial em relação a variável x.
- A expressão encontrada durante a computação representa a derivada de y em relação a x, isto é, "Dt[expressão,variável]" computa a derivada total.
- "Dt[expressão]" computa a diferencial total "d(expressão)".
Veja os exemplos a seguir, sobre os cálculos de derivadas das funções implícitas. A expressão "Dt[y,x]", encontrada durante a computação, representa a derivada de y em relação a x, isto é, Dt[y,x] = ![]() . Utilizamos o comando "Solve" para encontrar os resultados desejados.
. Utilizamos o comando "Solve" para encontrar os resultados desejados.
Exemplo 4.7
Calcular ![]() para as funções implícitas dadas a seguir:
para as funções implícitas dadas a seguir:
a) x2 ![]() y2 = 4;
y2 = 4;
b) ![]() .
.
Resolução
Resolvemos estes exemplos utilizando os seguintes comandos:
a) In[ ]:= Dt[x^2+y^2==4,x]
Out[ ]= 2 x + 2 y Dt[y, x] == 0
In[ ]:= Solve[Dt[x^2+y^2==4,x],Dt[y,x]]
Out[ ]= {{Dt[y, x] -> - (![]() )}}
)}}
b) In[ ]:= Solve[Dt[Exp[- (x^2+y^2)]==Log[x],x],Dt[y,x]]
Out[ ]= {{Dt[y, x] ->  }}
}}
Os mesmos resultados acima, podem ser obtidos utilizando o comando "D" do Mathematica se declararmos que y é uma função de x, isto é, se escrevemos y=y[x]. Veja os cálculos abaixo:
a) In[ ]:= D[x^2+y[x]^2==4,x]
Out[ ]= 2 x + 2 y[x] y'[x] == 0
In[ ]:= Solve[D[x^2+y[x]^2==4,x],y'[x]]
Out[ ]= {{y'[x] -> - (![]() )}}
)}}
b) In[ ]:= Solve[D[Exp[- (x^2+y[x]^2)]==Exp[- x],x],y'[x]]
Out[ ]= {{y'[x] ->  }}
}}
Assim, concluímos que
 , onde x2
, onde x2  y2 = 4;
y2 = 4;
 , onde
, onde  .
.
Derivadas parciais são calculadas utilizando o mesmo comando que foi utilizado para calcular a derivada, isto é, "D" ou "Derivative". Seja f(x,y) uma função diferenciável em relação às variáveis x e y. Utilizamos os seguintes comandos para os cálculos das derivadas parciais.
- O comando "D[f(x,y),variável]" computa a derivada parcial de f(x,y) em relação a variável x ou y.
- O comando "D[f(x,y),{variável,n}]" calcula a n-ésima derivada parcial de f(x,y).
- O comando "D[f(x,y),x,y]" calcula a derivada parcial de f(x,y) primeiro em relação a y e depois em relação a x. O comando "D[f(x,y),y,x]" calcula a derivada parcial de f(x,y) primeiro em relação a x e depois em relação a y.
- O comando "Derivative" também pode ser usado para calcular a derivada parcial da função.
- O comando "Derivative[1,0][f][a,b]" calcula a derivada parcial de f em relação a x e apresenta o resultado trocando x por a, e y por b.
- O comando "Derivative[0,1][f][a,b]" calcula a derivada parcial de f em relação a y e apresenta o resultado trocando x por a, e y por b.
- O comando "Derivative[n,m][f][a,b]" calcula a n-ésima derivada parcial da f em relação a x e depois a m-ésima derivada parcial de f em relação a y e apresenta o resultado trocando x por a, e y por b.
Veja alguns exemplos a seguir:
Exemplo 4.8
Calcular as derivadas parciais da função f(x,y) = ln(3x3![]() y)
y)![]() sen(x
sen(x![]() 3y3) em relação a x e y.
3y3) em relação a x e y.
Resolução
Utilizamos o comando "D" para calcular a derivada parcial. Podemos também derivar expressões que possuem variáveis independentes entre si. Assim sendo, assumimos que em "D[Log[3x3+y]+Sin[x+3y3],x]", y é independente de x, isto é, a derivada parcial de f(x,y) em relação a x é obtida utilizando o seguinte comando:
In[ ]:= D[Log[3 x^3+y]+Sin[x+3 y^3],x]
Out[ ]= 
Analogamente, a derivada da f(x,y) em relação a y é obtida por
In[ ]:= D[Log[3 x^3+y]+Sin[x+3 y^3],y]
Out[ ]= 
Observe que se y for dependente de x, podemos utilizar a forma funcional explícita y[x] e damos o seguinte comando:
In[ ]:= D[Log[3 x^3+y[x]]+Sin[x+3 y[x]^3],x]
Out[ ]= 
Assim, concluímos que

 ;
;
 .
.
Exemplo 4.9
Seja f(x,y) = (x3 ![]() y3)3/5. Calcular
y3)3/5. Calcular
a)  ;
;
b)  ;
;
Resolução
Utilizamos os seguintes comandos:
In[ ]:= Clear[f]
f[x,y]:=(x^3+y^3)^(3/5)
a) In[ ]:= D[f[x,y],x]
Out[ ]= 
In[ ]:= D[f[x,y],y]
Out[ ]= 
In[ ]:= D[f[x,y],y,x]
Out[ ]= 
Assim, concluímos que
 ;
; ;
; .
.
b) In[ ]:= Clear[f]
f[x,y]:=(x^3+y^3)^(3/5)
In[ ]:= D[f[x,y],{x,2}]
Out[ ]= 
In[ ]:= Together[%]
Out[ ]= 
In[ ]:= Together[D[f[x,y],{y,2}]]
Out[ ]= 
Assim, concluímos que
-
 =
=  ;
;
 =
=  .
.
Exemplo 4.10
Seja f(x,y) = log(x2![]() y2) cos(x
y2) cos(x![]() y). Calcular as seguintes derivadas parciais:
y). Calcular as seguintes derivadas parciais:
a) ![]() ,
, ![]() ,
, ![]() e
e ![]() ;
;
b) ![]() e
e ![]() ;
;
c)  e
e  .
.
Resolução
Utilizamos o comando "Derivative" para calcular as derivadas parciais desejadas. Em alguns casos achamos o mesmo resultado aplicando o comando "D". Inicialmente, definimos a função f(x,y).
In[ ]:= Clear[f]
f[x_,y_]:= Log[x^2+y^2] Cos[x+y]
a) In[ ]:= Derivative[1,0][f][x,y]
Out[ ]= 
![]()
ou
In[ ]:= D[f[x,y],x]
Out[ ]= 
![]()
In[ ]:= Derivative[0,1][f][x,y]
Out[ ]= 
![]()
ou
In[ ]:= D[f[x,y],y]
Out[ ]= 
![]()
In[ ]:= Derivative[1,1][f][x,y]
Out[ ]= 

ou
In[ ]:= D[f[x,y],x,y]
Out[ ]= 
![]() -
- 
In[ ]:= Derivative[1,1][f][y,x]
Out[ ]= 

ou
In[ ]:= D[f[x,y],y,x]
Out[ ]= 
![]() -
- 
Assim, concluímos que


 ;
;

 ;
;

 ;
;


 .
.
b) In[ ]:= Derivative[2,0][f][x,y]
Out[ ]= 

![]() In[ ]:= [Derivative[0,2][f][x,y]]
In[ ]:= [Derivative[0,2][f][x,y]]
Out[ ]= 

Assim, concluímos que


 ;
;


 .
.
c) In[ ]:= Derivative[2,1][f][Pi,Pi/2]
Out[ ]= ![]()
In[ ]:= N[%]
Out[ ]= -2.86925
In[ ]:= Derivative[1,2][f][Pi,Pi/2]
Out[ ]= ![]()
In[ ]:= N[%]
Out[ ]= - 2.67472
Assim, concluímos que
 = - 2.86925;
= - 2.86925; = - 2.67472.
= - 2.67472.
Iniciamos esta seção com a computação de integrais definidas e indefinidas. Apresentamos também exemplos de cálculo de integrais duplas e triplas. Vamos ver os comandos que serão utilizados para estes cálculos:
- O comando "Integrate[f[x],x]" calcula a integral indefinida
 .
.
- O comando "Integrate[f[x],{x,x1,x2}]" calcula a integral definida
 .
.
- O comando "Integrate[f[x,y],{x,x1,x2},{y,y1,y2}]" calcula a integral dupla definida
 .
.
- O comando "Integrate[f[x,y,z],{x,x1,x2},{y,y1,y2}],{z,z1,z2}]" calcula a integral tripla definida
 .
.
Quando "Integrate" não consegue produzir o resultado exato da expressão numa forma adequada, usamos "NIntegrate"; ou, simplesmente, utilizamos "N[%]" para achar o valor exato da expressão anterior. "NIntegrate" também é usado nos cálculos das integrais, onde "Integrate" não consegue calcular o valor da integral.
Exemplo 4.11
Calcular as seguintes integrais:
a) ![]() ;
;
b) ![]() .
.
Resolução
Utilizamos os seguintes comandos para resolver as integrais:
a) In[ ]:= Integrate[x^3+5 x^2+3 x- 5,x]
Out[ ]= ![]()
b) In[ ]:= Integrate[Log[x]/x^2,x]
Out[ ]= ![]()
Assim, concluímos que
-
 =
=  ;
;
 =
=  .
.
Exemplo 4.12
Calcular as seguintes integrais definidas:
a) ![]() ;
;
b)  ;
;
c)  .
.
Resolução
As integrais são resolvidas usando os seguintes comandos:
a) In[ ]:= Integrate[Cos[x],{x,0,Pi}]
Out[ ]= 0
b) In[ ]:= Integrate[(Sqrt[x^2+4])/x^3,{x,1,3}]
Out[ ]= ![]()
![]()
![]()
In[ ]:= N[%]
Out[ ]= 1.12235
c) In[ ]:= Clear[f]
f[x_]:=(2+3 x+5 x^2)/((1+x^2)(4+9 x^2))
NIntegrate[f[x],{x,0,2}]
Out[ ]= 0.788964
Resolvemos a mesma integral utilizando o processo de frações parciais:
In[ ]:= Apart[f[x]]
Out[ ]= 
In[ ]:= Integrate[%,{x,0,2}]
Out[ ]= ![]()
![]()
O valor numérico da integral calculada acima é obtido utilizando o comando "N[%]"
In[ ]:= N[%]
Out[ ]= 0.788964
Assim, concluímos que
 = 0;
= 0; = 1,12235;
= 1,12235; = 0,788964.
= 0,788964.
Exemplo 4.13
Calcular as seguintes integrais duplas:
a) ![]() ;
;
b) ![]() ;
;
c) ![]() .
.
Resolução
Para resolver integrais duplas sabemos que
![]() .
.
Partindo desta observação, calculamos as integrais usando os seguintes comandos:
a) In[ ]:= Integrate[y Cos[x]- x Cos[y],{x,0,Pi/2},y,0,Pi}]
Out[ ]= ![]() .
.
In[ ]:= N[%]
Out[ ]= 4.9348
b) In[ ]:= Integrate[x^2 y,{y,0,3},{x,1- 2 y,y^2}]
Out[ ]= ![]()
c) In[ ]:= NIntegrate[Cos[Exp[x y]],{x,0,1},{y,0,1}]
Out[ ]= 0.245001
Assim, concluímos que
 =
= ;
; =
= ;
; = 0,245001.
= 0,245001.
Exemplo 4.14
Calcular as seguintes integrais triplas:
a) ![]() ;
;
b) ![]() ;
;
Resolução
Para resolver integrais duplas sabemos que
![]() .
.
Partindo desta observação, calculamos as integrais triplas usando os seguintes comandos:
a) In[ ]:= Integrate[x y z,{x,1,2},{y,0,1},{z,1,3}]
Out[ ]= 3
b) In[ ]:= Integrate[y Exp[z],{y,1,2},{x,0,y^2}, {z,0,Log[x]}]
Out[ ]= ![]()
Assim, concluímos que
 = 3;
= 3; =
=  .
.
Observação
- No cálculo de integrais duplas e triplas deve-se cuidar na colocação dos limites das integrais nos comandos, isto é, quando uma variável está dependendo de outra, primeiro deve-se colocar os limites independentes e depois as variáveis dependentes. Veja a seguir os comandos:
 = Integrate[f(x,y,z),{x,a,b},{y,y(x1),y(x2)}, {z,z(y1),z(y2)}]
= Integrate[f(x,y,z),{x,a,b},{y,y(x1),y(x2)}, {z,z(y1),z(y2)}]
 = Integrate[f(x,y),{x,a,b},{y,y(x1),y(x2)}]
= Integrate[f(x,y),{x,a,b},{y,y(x1),y(x2)}]


